DL:常用最优化算法
编辑:佚名 日期:2024-07-08 21:26 / 人气:
- 背景
DL中,我们通过计算损失函数,来衡量当次迭代结果对应各个关键参数权重,在实际描述问题上的有效程度。通过损失函数的变化方向,来获取对应关键参数权重,更趋近于实际结果的梯度方向。从而被我们使用来更新当前参数权重配置,以降低损失函数值,逼近最优解。这一过程被称为一次迭代过程。而通过多次迭代来获取最优解的过程,被称为一次训练。
优化算法是一种更快实现权重逼近的处理办法。常用优化算法能够根据梯度方向和一些其他的关键信息,对当前权重作出更有效率的更新,降低训练所需要的迭代次数,同时提高模型鲁棒性。
1. SGD (stochastic gradient descent) 随机梯度下降法
迭代公式:
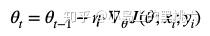
每次更新时,只对当前对应批次的被选用样本数据,进行Loss计算,一次计算一次更新。因为计算少,所以速度快,并且可以实现实时计算,支持动态的样本添加。
2. BGD (batch gradient descent) 批量梯度下降法
迭代公式:
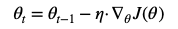
每次迭代需要计算当前批次整个数据集Loss,更新梯度。所以每次计算的耗时比较高。对于大批量数据来说,比较难以处理,更新不实时。简单的说,就是粒度太大。
3. MBGD (mini-batch gradient descent) 小批量梯度下降法
迭代公式:
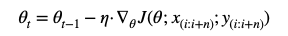
针对BGD每次都需要对当前批次数据集的问题,MBGD进行了改良,每一次更新,取当前批次中的一组子样本集合来进行Loss计算,降低参数更新方差计算,收敛更稳定,并且因为采用子批次构成矩阵运算,更加有优势。
Mark:基础优化算法比较
粒度: 小 SGD < MBGD < BGD 大
速度: 慢 BGD < MBGD < SGD 快
收敛: 低 SGD < MBGD < BGD 高
过拟合: 低 SGD < MBGD < BGD 高
因为SGD每次处理数据单取一个样本点,相比于MBGD的当前批次全数据取子集,和BGD当前批次扫描全部数据,SGD更新权重每次计算出的梯度变化幅度相对都会比较大一些,所以不容易在梯度更新上陷入局部最优解。这也是SGD较其余两种基本算法的最大优势。建议没有特殊要求,而需要在这三种算法中做选择的话,优先使用SGD。
当然,他们都有同样的缺点,那就是:
1. 仍存在易陷入局部最小值或鞍点震荡问题,以BGD为最
2. 仍存在无法根据不同参数重要程度进行变速权重更新问题,即所有权重更新速度统一问题。
1. Momentum 动量化
常用的减震算法,比较容易想到的就是利用阻尼运动特性和加速度(动量Momentum),来减小离散瞬时值的影响。因此,先贤们首先想到的就是梯度迭代动量化。
迭代公式:
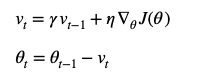
动量化是在原有计算权重迭代基础上,通过引入上一次变化值情况,来强化梯度延方向变化趋势。这样做可以使得梯度方向不变的维度,权重迭代速率加快,而方向发生改变的维度,更新速度变慢。并且由于速度此时变化是和之前状态有关系的,就不会发生“指向突变”的情况,有助于减小震荡和跃出鞍点。
超参数 γ 被称为阻尼系数,或遗忘因子,一般取 0.9,表示经验重要程度。
2. NAG 涅斯捷罗夫梯度加速
然而,单纯的动量处理却也存在其他问题。最明显的就是,因为动量叠加,没有修正逻辑的纯动量叠加,会导致每一次的轻微误差也随着时间一起叠加,导致当前时刻 t 时,实际梯度变化速率要远大于实际值,阻尼因子设定过小和初速度过大都可能会久久不能收敛。所以,在动量化的基础上,我们更希望能够有修正方法来减小误差的累积。幸运的是 Y Nesterov 在1983年提出的NAG很好的解决了这个问题。(详细推导过程可参考:https://zhuanlan.zhihu.com/p/22810533)
迭代公式:
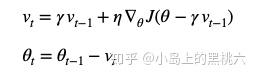
NAG较标准动量化处理来说,用来计算当前梯度方向的时候,计算Loss采用的是基于当前上一次梯度变化值预测的,当前状态下,下一次可能的维度权重。以这个预测的维度权重来计算当前位置的方向梯度变化,来修正动量化算法。这样,当我们计算当前 t 时梯度变化速度的时候,就可以从一定程度上避免掉误差堆积导致的问题。这里借用一下Hinton大佬的论文中的图来说明效果:

可以看出:
蓝色是 Momentum 的过程,会先计算当前的梯度,然后在更新后的累积梯度后会有一个大的跳跃。绿色是 NAG 会先在前一步的累积梯度上(brown vector)有一个大的跳跃,然后衡量一下梯度做一下修正(red vector),这种预期的更新可以避免我们走的太快。
1. AdaGrad 自适应梯度算法
迭代公式:

Gjj 为当前 参数 j 所对应的1到时刻 t 的所有梯度平方和。
可以看出,AdaGrad本质上是将SGD的统一学习速率修改为,有一定预测成分在内的,参数对应独立更新的处理方式。这样处理的好处是,每一个不同参数都会根据当前自身变化和总模型结果关系的差异,独立的进行变更,变化大的会更快,变化小的会更慢。减少了手动调节学习速率的次数。
缺点也比较明显:
1. 前期需要手工设置一个全局的初始学习率,过大值会导致惩罚变化不明显,过小会提前停止
2. 中后期自适应的分母会不断累积导致学习速率不断收缩,趋于非常小从而可能提前结束训练
因此,我们有了改进版
2. RMSprop 均方根传播法
迭代公式:
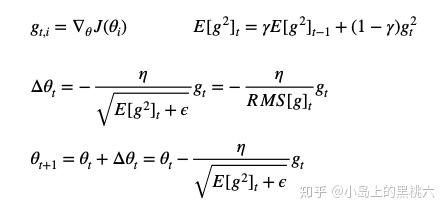
E[g2]t 为当前 参数j 所对应的1到时刻 t 的所有梯度均方和,有
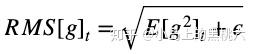
因为学习速率变化采用的是RMS,某一维度变化较大时,RMS较大;变化较小时,RMS较小。这样就保证了各个维度的变化速率是基于同一个变化量级的,同时也避免了AdaGrad 中后期的学习速率极速下降,过早停止的问题。而且,因为 RMS 采用近似算法,极大降低了内存消耗(毕竟不需要记录每一次的迭代值了)
不过,RMSprop可以看出,仍然依赖于全局学习速率 η 的设定,那么是否能够继续改进不依赖呢?
Mark:AdaGrad 和 RMSprop 单位问题
我们知道,很多问题是有实际含义的,可能是有单位的,比如是米,天等,所以 Δθt一个很自然的期望是,和 x 的单位是保持一致的。但是:

也就是说,对于AdaGrad 和 RMSprop来说,Δθt 权重变化量最终得到的结果,其单位和 θt 单 位并不一致,而是对应时间单位的倒数。而我们要的 权重 θt 是时间单位的。
如果我们使用牛顿法
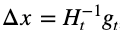
H 为 Hessian矩阵,即所有参数指定 t 时刻二阶偏导数方阵,有:
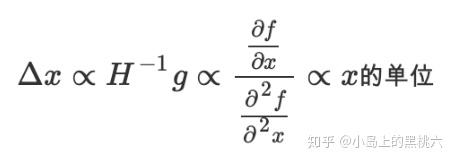
这样单位就一致了。但是Hessian矩阵计算量太大,我们没办法直接使用,所以,我们来模拟牛顿法,有:
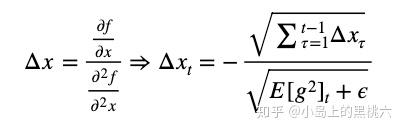
在∞位置近似等价。这样就可以保证单位一致性。同时我们发现,Δθt 的更新,在这种拟合处理 上,后续迭代不再依赖于全局学习速率 η 。
3. AdaDelta 自适应梯度算法改进版
迭代公式:
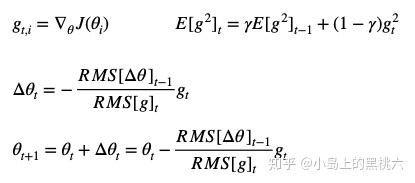
E[g2]t 为当前 参数j 所对应的1到时刻 t 的所有梯度均方和,有
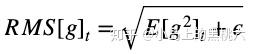
相较于前两种,AdaDelta 具有优势:
1. 结合了Adagrad善于处理稀疏梯度和RMSprop善于处理非平稳目标的优点
2. 不需要依赖于 全局学习速率的设置
这里引用一下特斯拉人工智能主管 Andrej Karpathy 的Demo 来做一下演示,大家感兴趣可以自己上这个网站上试一哈~~
ConvNetJS Trainer Comparison on MNIST直接上结果:
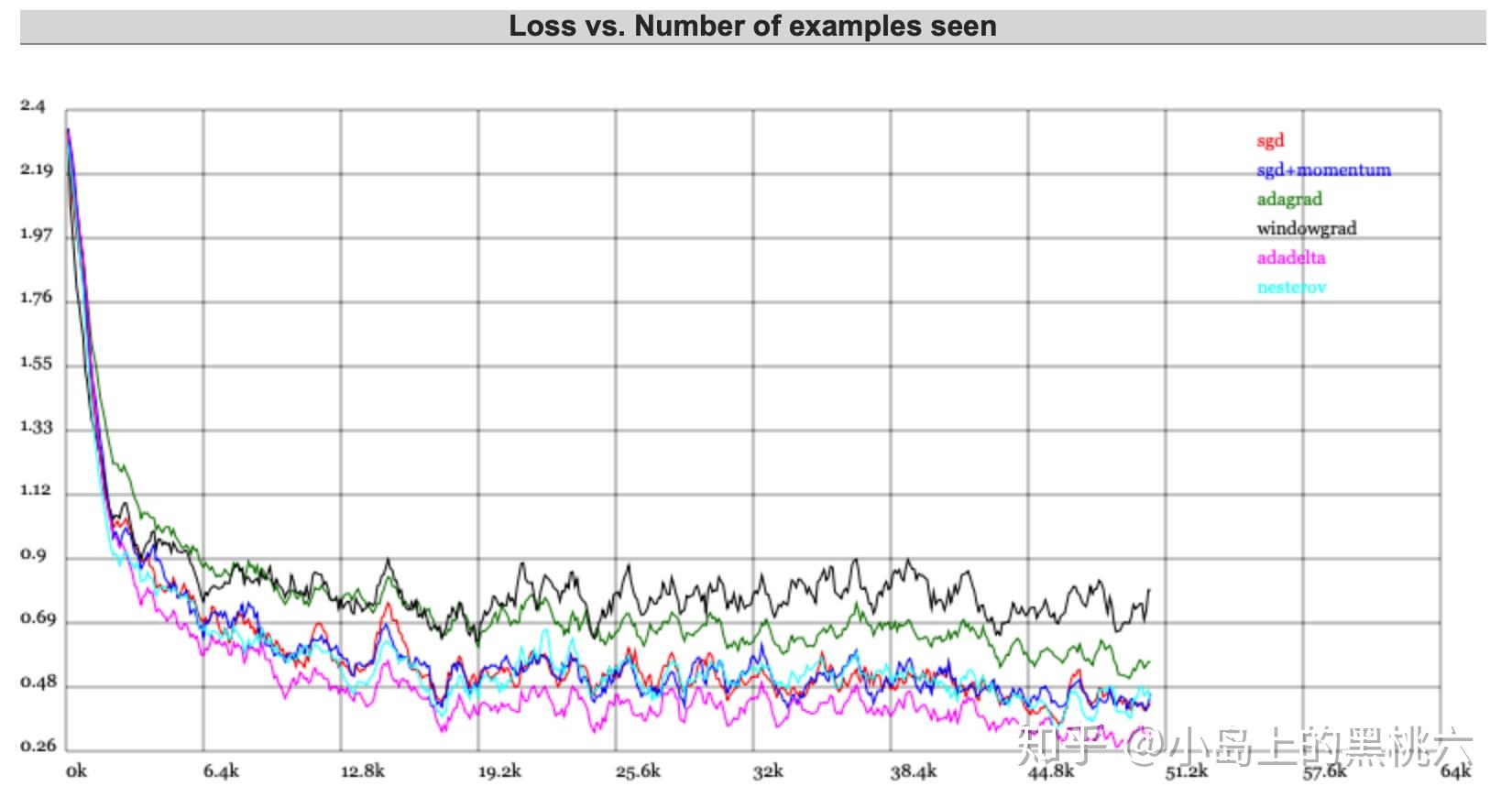
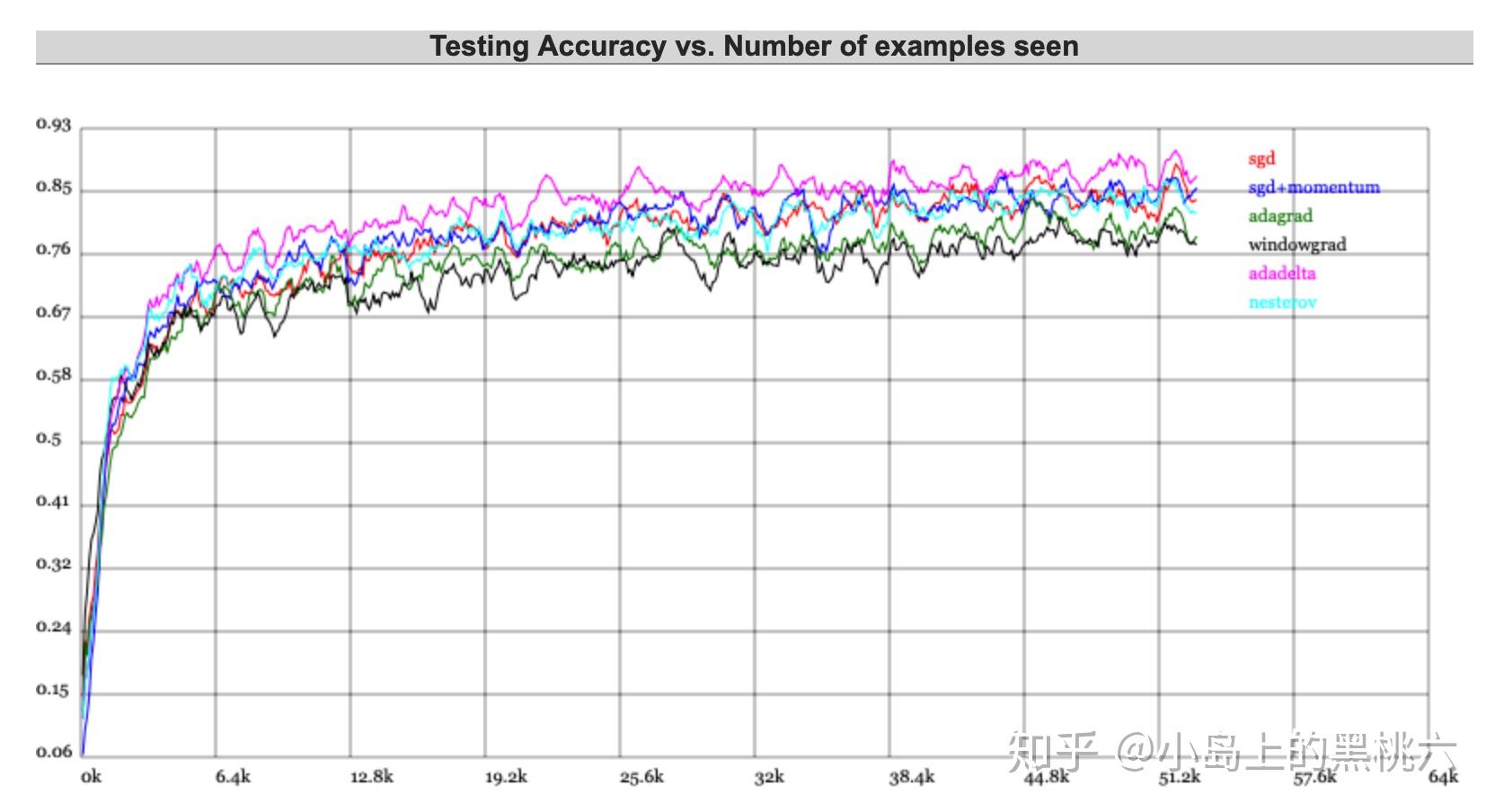
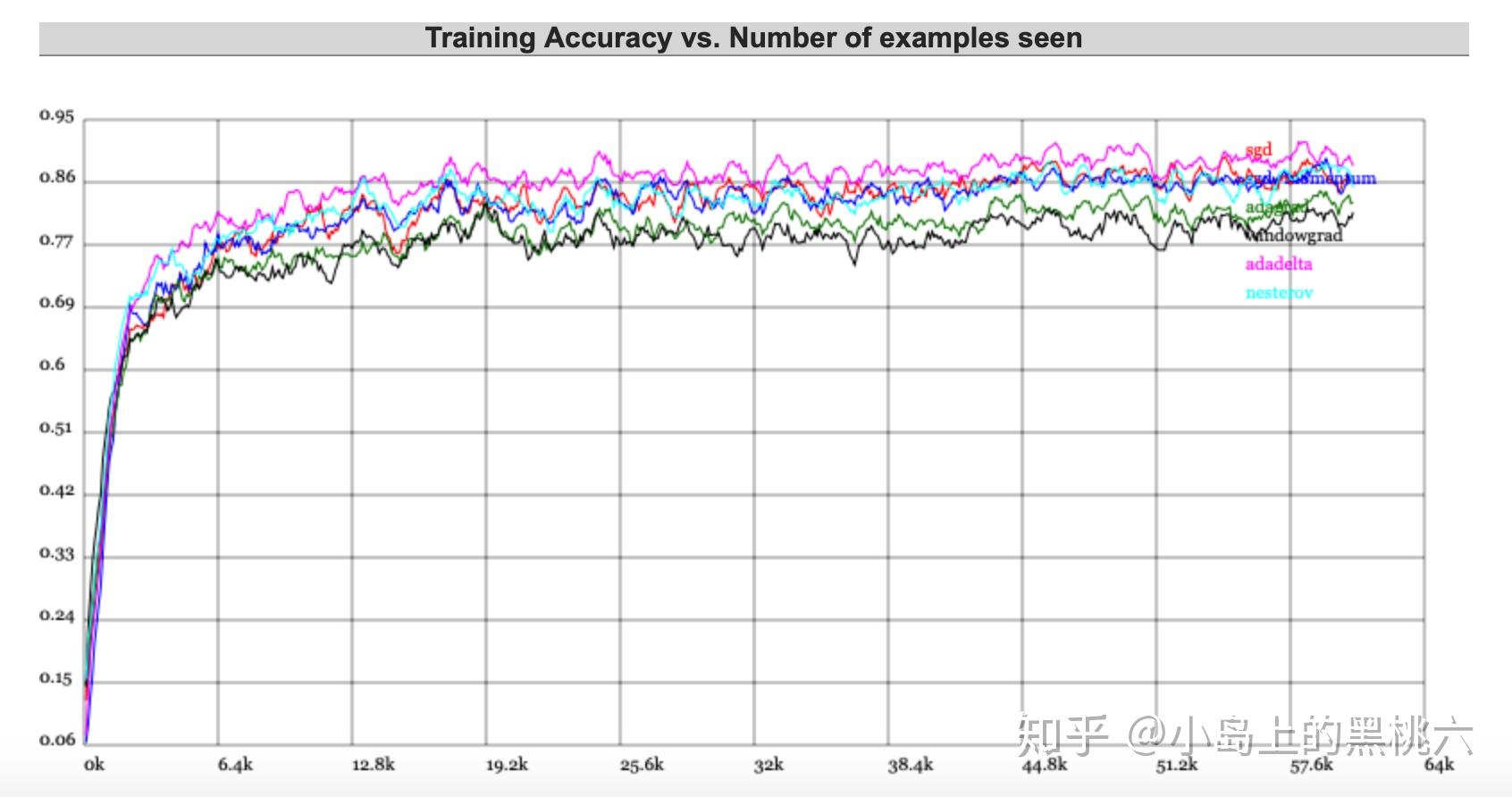
这个不太明显的话,我们还可以更直观一点~哈哈哈~

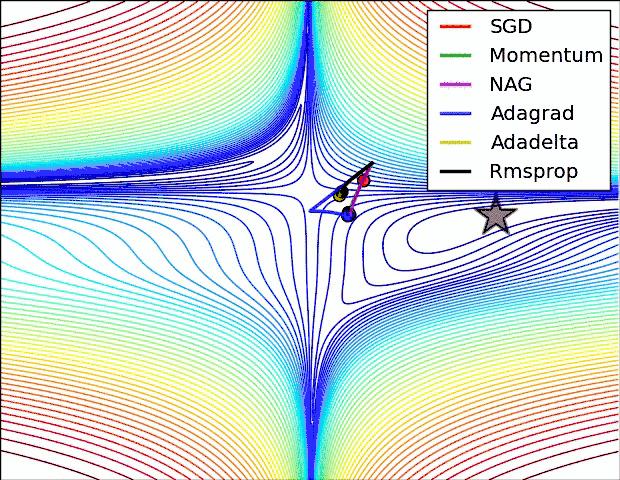
那么有没有什么方法,可以结合 Momentum 和 AdaDelta 的优点呢?既解决鞍点,又能自适应学习速率呢?当然有~那就是Adam
Adam (Adaptive Moment Estimation)自适应实时评估算法,相当于RMSprop 和 Momentum 结合的一种算法,标准Adam 可以认为是 一阶AdaDelta 的动量改进版。
迭代公式:

其中,我们为了防止 m、v 被初始化时为0导致向0偏移而做的偏差校正值,有:
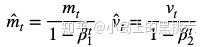
β1、β2 都是经验系数,Hinton建议 β1 = 0.9,β2 = 0.999
? 是防爆因子,建议? = 10e?8 避免干扰运算
Adam 很好的结合了前辈们的各种优化处理手段,成为了集大成之优化函数。因此,Adam也是现在主流优化函数之一。
至此,常用优化算法基本梳理完毕。
如果数据稠密,实际上简单的算法就能得到鲁棒性很好 的结果,这时候我感觉应该使用 SGD+Momentum 或 MBGD+Momentum 就能很好的处理得到结果,加动量既可以保证相对快的训练速度,也可以一定程度避免局部最小值。
如果数据稀疏,因为需要对关键特征点进行提取,所以需要用一些自适应算法,对于简单凸性和数据不复杂的算法,可以采用L1、L2正则化+组合分桶,复杂一些的,就需要采用Adagrad, Adadelta, RMSprop, Adam。
如果关键参数更多的出现在运算后期,即梯度稀疏一定程度后,则Adam 比 RMSprop 效果会好。这是后Adam明显是最好的选择~
到目前业界前辈、各路大佬,还在不断探索更优秀优化算法、专精特殊处理改进版本、已有算法的优化处理。希望未来能够见证新的奇迹诞生。
参考文献:
An overview of gradient descent optimization algorithms (https://ruder.io/optimizing-gradient-descent/index.html#fn6)
H. Robinds and S. Monro, “A stochastic approximation method,” Annals of Mathematical Statistics, vol. 22, pp. 400–407, 1951.
Nesterov, Y. (1983). A method for unconstrained convex minimization problem with the rate of convergence o(1/k2). Doklady ANSSSR (translated as Soviet.Math.Docl.), vol. 269, pp. 543– 547.
内容搜索 Related Stories
推荐内容 Recommended
- 学习法律法规心得体会范文09-23
- 哪个平台提供原创带货视频?这些平台靠谱吗?09-23
- 山东电子竞技运动与管理专业大学排名及录取分数线(2025高考参考)09-23
- 【N4文法】~れる/られる/される(受身/受動態)09-23
- 生物药研发总监岗位职责08-14





