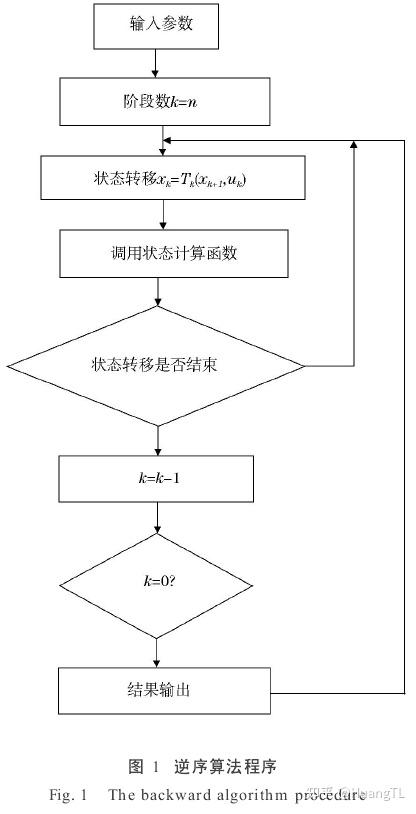
优化算法---动态规划
编辑:佚名 日期:2024-05-26 09:11 / 人气:
动态规划(Dynamic Programming)是根据“最优决策的任何截断仍是最优的”这一原理,通过将多阶段决策过程转化为一系列单阶段问题,逐个求解的优化求解方法.
目前常用的方法有逆序、顺序以及双向混合算法.
构造一个标准的动态规划模型,通常需要采用以下几个步骤:
- 划分阶段:按照问题的时间或空间特征,把问题分为若干个阶段.这些阶段必须是有序的或者是可排序的(即无后向性),否则,应用无效.
- 选择状态:将问题发展到各个阶段时所处的各种客观情况用不同的状态表示,称为状态.状态的选择要满足无后效性和可知性,即状态不仅依赖于状态的转移规律,还依赖于允许决策集合和指标函数结构.
- 确定决策变量与状态转移方程:当过程处于某一阶段的某个状态时,可以做出不同的决策,描述决策的变量称为决策变量.在决策过程中,由一个状态到另一个状态的演变过程称为状态转移.
- 写出动态规划的基本方程:动态规划的基本方程一般根据实际问题可分为两种形式,逆序形式和顺序形式.
动态规划基本方程的逆序形式为:
其中第 阶段的状态为
,其决策变量
表示状态处于
的决策,状态转移方程为
,
阶段的允许决策集合记为
为指标函数.
当求解时,由边界条件从 开始,由后向前逆推,逐阶段求出最优决策和过程的最优值,直到最后求出
即得到问题的最优解.
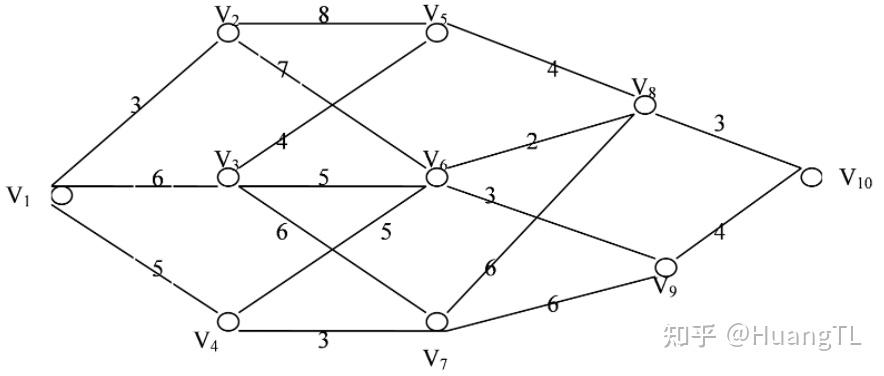
计算由V1到达V10的最短路径。
即函数中的参数S,S以矩阵形式被表示,空缺部分使用nan补齐;
就该图片而言,我们将其分成5个阶段,每个阶段含有的状态变量分别为{V1},{V2,V3,V4},{V5,V6,V7},{V8,V9},{V10}转化为matlab内矩阵形式即为:

相应代码:
S=nan.*ones(3,5);
S(1,1)=1;
S(1:3,2)=[2;3;4];
S(1:3,3)=[5;6;7];
S(1:2,4)=[8;9];
S(1,5)=10;代入阶段k及状态变量s求出允许决策集合函数
可以简单的使用switch构造:
如图中case 1,u=[2;3;4];表明节点V1的下一个节点可以为V2,V3,V4,由于该实例较为简单,这里实际上只使用的了s一个参数,k参数的引入可以刻画更加复杂的问题,这里不展开讨论。
function u=dpMinDis_DecisFun(k,s)
switch s
case 1,u=[2;3;4];
case 2,u=[5;6];
case 3,u=[5;6;7];
case 4,u=[6;7];
case 5,u=8;
case 6,u=[8;9];
case 7,u=[8;9];
case 8,u=10;
case 9,u=10;
case 10,u=10;
end
end在该题中指的便是两点之间的路长,例如case (s==6&u=8),v=2;即为V6和V8点之间距离为2。同样由于实例较为简单并未使用参数k。
function v=dpMinDis_SubObjFun(k,s,u)
v=inf;
switch 1
case (s==6&u==8),v=2;
case (s==1&u==2)|(s==4&u==7)|(s==6&u==9)|(s==8&u==10),v=3;
case (s==3&u==5)|(s==5&u==8)|(s==9&u==10),v=4;
case (s==1&u==4)|(s==3&u==6)|(s==4&u==6),v=5;
case (s==1&u==3)|(s==3&u==7)|(s==7&u==8)|(s==7&u==9),v=6;
case (s==2&u==6),v=7;
case (s==2&u==5),v=8;
end
end ;对于该题来说,实际上
就是
,本例中该函数可以省略;
function s=dpMinDis_TransFun(k,s,u)
s=u;
end当前问题下f没有劳损或增值等因素,故直接采用f=v+f
function f=dpMinDis_ObjFun(v,f)
f=v+f;
end通过如下方式进行程序调用:
[opt,fval]=dpReverse(S,@dpMinDis_DecisFun,@dpMinDis_SubObjFun,@dpMinDis_TransFun,@dpMinDis_ObjFun)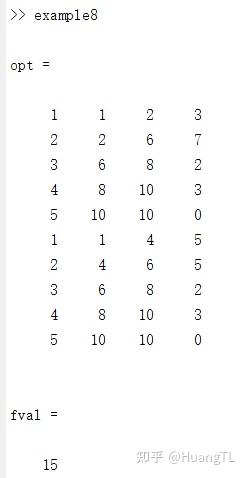
其中opt为最优路径,fval为最短距离,我们详细来看opt结果,opt最左列是用来区分路径的序号,它由1增长到5之后再次由1增长到5,说明最优结果包含两条路径,且都经过了五个点,
opt中
第二列是每一段路的起点
第三列是每一段路的终点
第四列是每一段路的路长
如图所示,下图第一行表示最短路首先由点1到达点2且经过距离为3,而整幅图说明最短路为:
1—>2—>6—>8—>10
且最短路长为3+7+2+3+0=15

因此我们从计算结果opt可以看出,该题有两个最短路,分别为:
1—>2—>6—>8—>10
1—>4—>6—>8—>10
最短路长为15
% dynamic programming
S=nan.*ones(3,5);
S(1,1)=1;
S(1:3,2)=[2;3;4];
S(1:3,3)=[5;6;7];
S(1:2,4)=[8;9];
S(1,5)=10;
[opt,fval]=dpReverse(S,@dpMinDis_DecisFun,@dpMinDis_SubObjFun,...
@dpMinDis_TransFun,@dpMinDis_ObjFun)
function[opt,fval]=dpReverse(S,DecisFun,SubObjFun,TransFun,ObjFun)
%动态规划逆序法
%变量或函数名 类型 释义
%--------------------------------------------------------------------------
% S | 矩阵 | 状态变量,每一列代表一个阶段的状态,空缺处用NAN补齐
% DecisFun(k,s) | 函数 | 代入阶段k及状态变量s,返回s下一状态的集合
% TransFun(k,s,u) | 函数 | Tk(sk,uk),其中s是阶段k的状态,u是相应的决策变量
% SubObjFun(k,s,u)| 函数 | 阶段指标函数 V(sk,uk)
% ObjFun(v,f) | 函数 | 第k阶段直到最后阶段的指标函数
% opt | 矩阵 |[序号,最优策略,最优轨线,指标]
% fval | 数值 | 最优解数值
%第一阶段:变量初始化======================================================N=sum(sum(~isnan(S))); %节点总数量
opt_F=ones(1,N).*inf; %存储当前节点到达最终阶段最短距离
opt_U=ones(N,N).*inf;
opt_V=ones(N,N).*inf;
ePnt=S(:,size(S,2)); %取出最终节点所在列数据
ePnt(isnan(ePnt))=[]; %取出最终节点
opt_F(ePnt)=0; %每一节点到达最终节点最短距离
opt_U(1,ePnt)=ePnt; %每一节点对应最优下一节点集合
opt_V(1,ePnt)=0; %每一节点对应最优下一节点距离
%第二阶段:动态规划逆序求解================================================%注:程序中以大写字母开头的变量表示集合,小写字母开头变量表示元素
for k=size(S,2)-1:-1:1
Sk=S(:,k);
Sk(isnan(Sk))=[]; %Sk:第k阶段节点集合(状态变量)
for sk=Sk'
%返回 sk 下一状态所有可能集合
Uk=feval(DecisFun,k,sk); %执行 DecisFun(k,sk) -> dpMinDis_DecisFun(k,sk)
%返回 sk 下一状态所有可能集合(本例中下面一行代码注释掉不影响)
Uk=feval(TransFun,k,sk,Uk); %Uk:允许决策集合
F=ones(1,length(Uk)).*inf; %F:指标集合
V=ones(1,length(Uk)).*inf; %V:阶段指标集合
for i=1:length(Uk)
uk=Uk(i);
v=feval(SubObjFun,k,sk,uk); %sk到达uk距离 %计算从状态 sk->uk 所用的cost
f=feval(ObjFun,v,opt_F(uk)); %sk经过uk到底最终阶段点距离 %计算从状态 sk->uk_>最终节点 所用的最小总cost
F(i)=f; %记录sk通过各个uk到达最终阶段最短距离
V(i)=v; %记录sk到各个uk距离
end
opt_pos=find(F==min(F)); %寻找最短的f所对应的uk
opt_F(sk)=min(F); %寻找最短的f所对应的到达最终阶段最短距离
opt_U(1:length(opt_pos),sk)=Uk(opt_pos)'; %每一节点对应最优下一节点集合
opt_V(1:length(opt_pos),sk)=V(opt_pos)'; %每一节点对应最优下一节点距离
end
end
%第三阶段:路径还原========================================================sPnt=S(:,1);
sPnt(isnan(sPnt))=[];
Path=zeros(1,size(S,2)+1);
Path(1)=sPnt; %将路径的第一个点设置为起始点
for i=1:size(S,2) %经过size(S,2)个阶段
NewPath=zeros(1,size(S,2)+1);
NewPath(:,:)=[];
for j=1:size(Path,1)
branch=opt_U(:,Path(j,i));
branch(isinf(branch))=[]; %获取当前路径最后一个节点的下一个节点
for m=branch'
tempPath=Path(j,:); %复制之前路径
tempPath(1,i+1)=m; %将之前路径中下一个节点添加到路径
NewPath=[NewPath;tempPath]; %每多一个分支多派生出一条路径
end
end
Path=NewPath;
end
%将路径整理形状并拼成矩阵
temp_n=reshape((1:size(S,2))'*ones(1,size(Path,1)),size(S,2)*size(Path,1),1);
temp_s=reshape(Path(:,1:size(S,2))',size(S,2)*size(Path,1),1);
temp_e=reshape(Path(:,2:size(S,2)+1)',size(S,2)*size(Path,1),1);
for i=1:length(temp_n)
coe=opt_U(:,temp_s(i))==temp_e(i);
temp_v(i,1)=opt_V(coe,temp_s(i));
end
opt=[temp_n,temp_s,temp_e,temp_v];
fval=sum(opt(1:size(S,2),4));
end
function u=dpMinDis_DecisFun(k,s)
switch s
case 1,u=[2;3;4];
case 2,u=[5;6];
case 3,u=[5;6;7];
case 4,u=[6;7];
case 5,u=8;
case 6,u=[8;9];
case 7,u=[8;9];
case 8,u=10;
case 9,u=10;
case 10,u=10;
end
end
% 计算从状态 s->u 所用的cost
function v=dpMinDis_SubObjFun(k,s,u)
v=inf;
switch 1
case (s==6&u==8),v=2;
case (s==1&u==2)|(s==4&u==7)|(s==6&u==9)|(s==8&u==10),v=3;
case (s==3&u==5)|(s==5&u==8)|(s==9&u==10),v=4;
case (s==1&u==4)|(s==3&u==6)|(s==4&u==6),v=5;
case (s==1&u==3)|(s==3&u==7)|(s==7&u==8)|(s==7&u==9),v=6;
case (s==2&u==6),v=7;
case (s==2&u==5),v=8;
end
end
function s=dpMinDis_TransFun(k,s,u)
s=u;
end
function f=dpMinDis_ObjFun(v,f)
f=f+v;
end基于MATLAB的动态规划常用算法的实现---孙 宝 王希云
基于MATLAB的动态规划逆序算法的实现---孙晓君





