先来回顾一下神经网络的经典结构，如下图所示：

一般神经网络分为：输入层，隐藏层，输出层。上图中的连线代表的是神经网络中的参数，参考下面的图：

常用的激活函数有：

如果对上面的内容有疑惑的话，可以参考笔者的上一篇文章《谈谈对神经网络的理解 “谈谈对神经网络的理解”》，这里不再赘述。

好了，下面进入正题。

在讲优化算法之前，我们先要明确损失函数的概念，损失函数有很多种说法，中文也可以叫代价函数或者目标函数，英文中有 loss function, cost function, objective function. 实际上指得是同一个概念。

首先，神经网络是用来解决实际问题的，我们以分类问题来举例。假设我们要做图片的猫狗分类，即输入一张图片，判断是猫还是狗。

神经网络只能输出数值，没办法输出概念，所以需要对猫狗概念做一个转化，类似于数学建模。我们可以令网络输出为 0 时代表猫，输出为 1 时代表狗。不过就像世界不是非黑即白一样，有时候我们需要的也不是这样一个非 0 即 1 的输出，我们希望知道神经网络认为输入图片是狗的概率值，所以我们设计神经网络的输出为 [0, 1] 之间的浮点数，其数值就代表输入图片是狗的概率。若输入图片是狗，我们希望神经网络的输出越大越好；反之，若输入图片是猫，则我们希望神经网络的输出越小越好。

前面我们是以定性的方式评判神经网络的输出（越大越好或越小越好），但计算机只认数字，所以我们要将定性评判方式改为定量评判方式，即用损失函数来取代前面的越大越好或越小越小这样的定性说法。

最简单的损失函数的均方差损失函数（Mean Squared Error，MSE），如下所示：

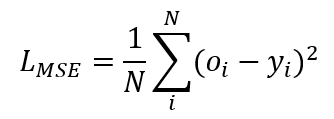
其中，N 是样本是数目，o 是神经网络输出，y 是真实值。那么为什么用平方差来作为误差的衡量，而不是直接用差的绝对值呢？这是因为绝对值在求导数时不方便，而平方计算求导数时简单方便（至于为什么需要求导数，后文会讲）。

使用均方差损失函数可以很容易的衡量神经网络分类效果的好坏，当均方差为 0 时，说明神经网络 100% 分类正确，均方差越大，说明错误越多。

除了均方差损失函数，还有很多其他常用的损失函数，比如交叉熵损失函数（Cross entropy），这里不展开细讲，读者只需要理解损失函数是对神经网络输出结果好坏的定量评判。针对不同的任务，我们会使用不同的损失函数。

为了更好的理解损失函数的性质，我们可以对其进行可视化。前面我们知道，损失函数是对神经网络输出的定量评判，所以损失函数实际上是神经网络参数的函数。受限于人类的感官，我们以二维情况举例，假设神经网络只有 w1, w2 两个参数，即

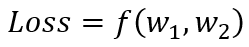
其中，f 代表的神经网络的运算集合。

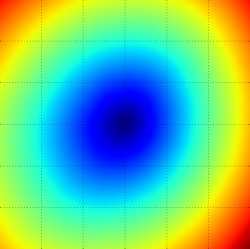
分别以 w1, w2 为 x, y 轴，用颜色代表 Loss 大小，可以在二维平面画出损失函数的图像，如下所示：[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-RWeREJ6f-1572681941001)(http://km.oa.com/files/photos/pictures//20190119//1547885188_94.png)]
中间的黑色代表损失函数最小的位置，也是我们的优化目标。

神经网络优化问题实际是寻找损失平面上的最低点过程。有一个很好的比喻：想象你处在半山腰，优化过程就是你到达山底的过程，如下图所示。

如果我们有地图的话，我们可以非常简单的直奔山底而去，但非常可惜，你的周围是一篇黑暗，你只能看清脚下，其他地方是什么样子一概不清楚，这种情况下我们该怎样找到山底呢？

最简单的办法就是随机搜索：不断地随机走，记录走过的最低位置。实现起来也非常简单：

但很明显，这不是一个好办法，费时费力还不一定有好效果。

再仔细想一想，想最快的到达最低点，我们该怎么做呢？如果我们看清周围的环境，我们肯定会选择向下走，而不是向上走，用数学语言来说，我们会选择斜率最大的方向走，如下图所示。

在没有地图的情况下，沿斜率最大的方向走是一种贪心算法，不一定能到达全局最优，但一定可以收敛到局部最优解。

前面提到的沿斜率最大的方向走其实有一个更加专业的说法，叫做“梯度下降法”。学过微积分就知道函数导数的定义为：

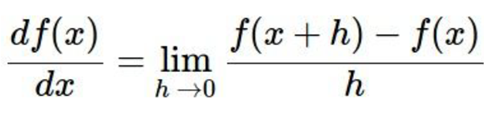
梯度的定义为该点在各个维度导数最大的方向。

我们只要沿着负梯度方向走，就能最快的收敛到最低点，在损失平面的示例如下图所示。

所以，当我们处在损失平面的一个位置时，先求出这个位置的梯度方向，然后我们只需要沿着负梯度方向前进就可以了。但是，这里还有一个问题，方向我们确定了，我们该走多远呢，或者说步长是多少？
这个问题主要有两种解决办法，一种是指定步长；一种是自适应步长。对应的也有很大不同的优化算法，下面逐一进行讲解。

另外，步长其实也有一个更加专业的说法，叫做 “学习率（Learning Rate）”，通常喜欢用 η 表示。

批量梯度下降，每次取全部的样本计算梯度，然后再更新参数，其学习率是固定的，参数更新公式为：

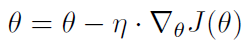
其中 θ 是网络参数， η 表示学习率，J 是损失函数，▽ 是求导符号。上面的公式就表示在负梯度方向更新参数。

随机梯度下降， 每次取 1 个样本计算梯度，公式为：

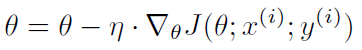
因为每次只计算一个样本，所以 SGD 计算非常快并且适合线上更新模型。但是，频繁地更新参数也使得损失函数抖动非常厉害，如下图。

小批量梯度下降，综合前面两种算法，每次取一个小批量样本计算梯度，公式如下：

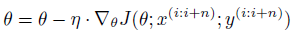
每次取小批量样本训练是训练神经网络的标准做法，小批量样本大小一般叫做 batch size，数值从 8 到 2048 都有，属于可调节的超参数。这种做法的好处是：

• 相比较 SGD 增加了一次更新使用的训练数据量，使得目标函数收敛得更加平稳；
• 可以使用矩阵操作对每批数据进行计算，大大提升了算法的效率。

前面三种都是标准梯度下降法，只是在每次计算的样本大小上做文章。下面的优化算法可以理解为在 Mini-Batch GD 的基础加入一些 trick，解决 Mini-Batch GD 存在的一些问题。

实际中，我们遇到的目标函数往往在不同的维度上梯度相差很大，比如在下面的函数等高线图中可以看出函数在纵向上要比横向陡峭得多。

SGD 等基本梯度下降算法并不知道这些，因为 y 方向梯度大 x 方向梯度小所以它们会在 y 方向上不断摇摆而沿 x 方向缓慢移动，但是我们知道在 y 方向的震荡是无用的只有 x 方向的才在不断接近最优点。

Momentum 是模拟物理里动量的概念，积累之前的动量来替代真正的梯度。公式如下：

其中，γ 是动量因子，一般取 0.9。

由于目标函数在 y 方向上摇摆，所以前后两次计算的梯度在 y 方向上相反，所以相加后相互抵消，而x方向上梯度方向不变，所以x方向的梯度是累加的，其效果就是损失函数在 y 方向上的震荡减小了，而更加迅速地从 x 方向接近最优点。

也可以把这个过程和在斜坡放一个球让其滚下类比：当从斜坡顶端释放一个小球时，由于重力的作用小球滚下的速度会越来越快；与此类似，冲量的作用会使相同方向的梯度不断累加，不同方向的梯度相互抵消，其效果就是逼近最优点的速度不断加快。

想象小球从山坡上滑落，它的速度沿着山坡不断加快，然而这并不是令我们满意的结果，当小球接近山谷（最优点）时，它已经有了很大的速度，很可能会再次冲向山谷的另一边，而错过了最优点。我们需要一颗更加“聪明”的小球，它能够感知坡度的变化，从而在它再次冲上山坡之前减速而避免错过山谷。

Nesterov accelerated gradient（NAG）就是一种让小球变“聪明”的方法。NAG 公式如下：

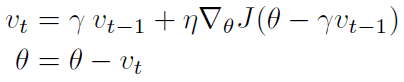
其中，γ 是动量因子，一般取 0.9。

跟上面 Momentum 公式的唯一区别在于，梯度不是根据当前参数位置 θ，而是根据先走了本来计划要走的一步后，达到的参数位置 θ - γv_t-1 后计算出来的。

对于这个改动，很多文章给出的解释是，能够让算法提前看到前方的地形梯度，如果前面的梯度比当前位置的梯度大，那我就可以把步子迈得比原来大一些，如果前面的梯度比现在的梯度小，那我就可以把步子迈得小一些。这个大一些、小一些，都是相对于原来不看前方梯度、只看当前位置梯度的情况来说的。

NAG 本质上是多考虑了目标函数的二阶导信息，所以可以加速收敛。其实所谓“往前看”的说法，在牛顿法这样的二阶方法中也是经常提到的，比喻起来是说“往前看”，数学本质上则是利用了目标函数的二阶导信息。

如上图所示，Momentum 首先计算一个梯度（短的蓝色向量），然后在前一步的更新方向上进行一个大的跳跃（长的蓝色向量）。Nesterov 首先在前一步的更新方向上进行一个大的跳跃（棕色向量），然后在跳跃后的点计算梯度（红色向量），得到最终更新方向（绿色向量）。

分析上面的原理可知，当“小球”将要冲上山坡的另一面时，红色线表示的预测梯度方向发生改变，从而将棕色向量往回拉达到了“减速”的效果。

前面讲的都是学习率固定的优化算法，Adagrad 是第一个自适应学习的优化算法。

Adagrad 是一种适合处理稀疏特征的梯度更新算法，它对稀疏特征采用高的更新速率，而对其他特征采用相对较低的更新速率。Dean 等人发现 Adagrad 能很好地提高 SGD 的鲁棒性，它已经被谷歌用来训练大规模的神经网络。

Adagrad 公式为：

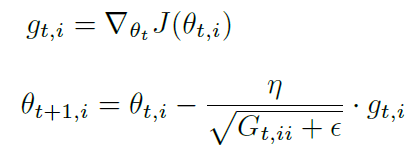
G 为对角矩阵，对角元素为该维度参数的梯度平方和。写成向量形式：

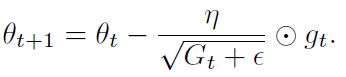
Adagrad 的优点是自适应学习率，Adagrad 主要缺点是累加了参数的历史梯度的平方，所以到后期学习率会越来越小，最后无法再学习到新的信息。下面介绍的算法就是来解决这个问题的。

Adadelta 主要解决了 Adagrad 算法中学习率衰减过快的问题，它不再累加参数所有的历史梯度平方和，转而设定一个窗口 w，只求前 w 个历史梯度平方的平均数，并且也不直接存储这些项，仅仅是近似计算对应的平均值。即：

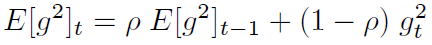
ρ 参数类似于 Momentum 的动量项，一般取为 0.9，Adadelta 的更新项为

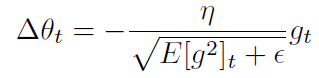
分母是 Root Mean Squared（RMS），所以上式可以记为：

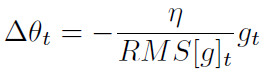
The authors note that the units in this update (as well as in SGD, Momentum, or Adagrad) do not
match, i.e. the update should have the same hypothetical units as the parameter. To realize this, they first define another exponentially decaying average, this time not of squared gradients but of squared parameter updates: （关于这一段的具体解释参考 Adadelta 论文 3.2 节）

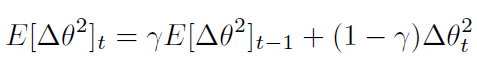
Δθ 的 RMS 为

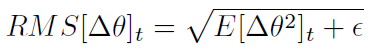
Adadelta 的更新公式为

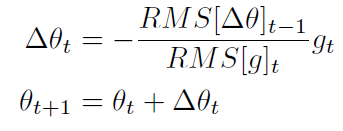
可以看出 Adadelta 不依赖全局学习率。

RMSprop 是 Geoff Hinton 提出的，与 Adadelta 类似，也是为了解决 Adagrad 学习率单调下降的问题。RMSprop 和 Adadelta 是同时独立提出来的。

RMSprop 跟 Adadelta 的第一版公式相同，更新公式为：

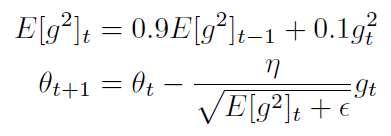
Hinton 建议 γ 参数设为 0.9，学习率 n 设为 0.001。

Adam（Adaptive Moment Estimation）本质上是带有动量项的 RMSprop，它利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率。Adam 的优点主要在于经过偏置校正后，每一次迭代学习率都有个确定范围，使得参数比较平稳。

mt and vt are estimates of the first moment (the mean) and the second moment (the uncentered
variance) of the gradients respectively, hence the name of the method. As mt and vt are initialized as vectors of 0’s, the authors of Adam observe that they are biased towards zero, especially during the initial time steps, and especially when the decay rates are small (i.e. 1 and 2 are close to 1).

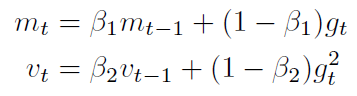
They counteract these biases by computing bias-corrected first and second moment estimates: （由于当 β1， β2 接近于1时，上面两项接近 0，所以用下面的式子进行偏差修正）

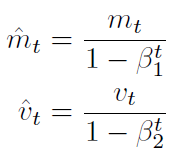
They then use these to update the parameters just as we have seen in Adadelta and RMSprop, which yields the Adam update rule:

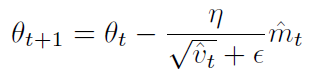
作者建议 β1 默认 0.9，β2 默认 0.999，ε 默认 10^-8。

Adam 应该是目前最流行的优化算法，效果非常稳定。

Adam vt 的更新使用了梯度的二范式，可以推广为 p 范式的形式：

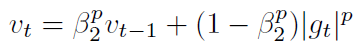
p 很大时，数值不稳定，所以 1-范式，2-范式比较常用。但是无穷范式也是数值稳定的，Adamax 就是用的无穷范式：

Adamax 的参数更新公式为：

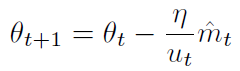
作者建议 β1 默认 0.9，β2 默认 0.999，η 默认 0.002。

下图展示了各个算法在 loss 等高线上的优化过程。

可以看到，Adagrad, Adadelta, RMSprop 收敛最快。SGD, Momentum, NAG 开始的方向都是错误的，但 NAG 最先找到正确的方向。

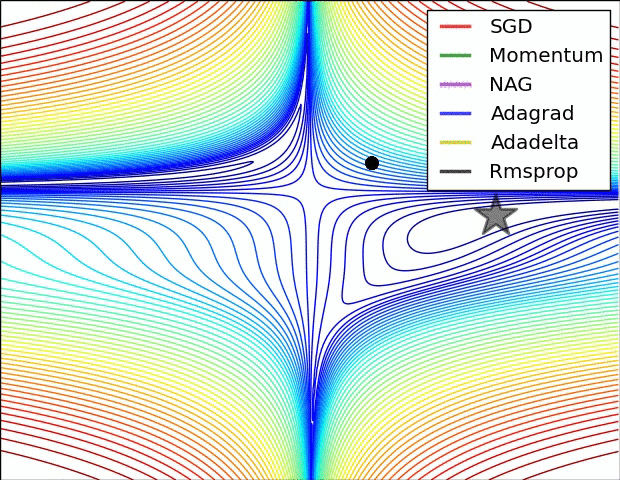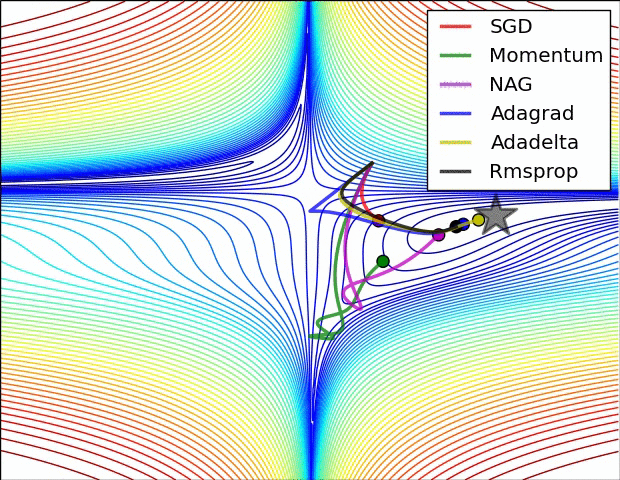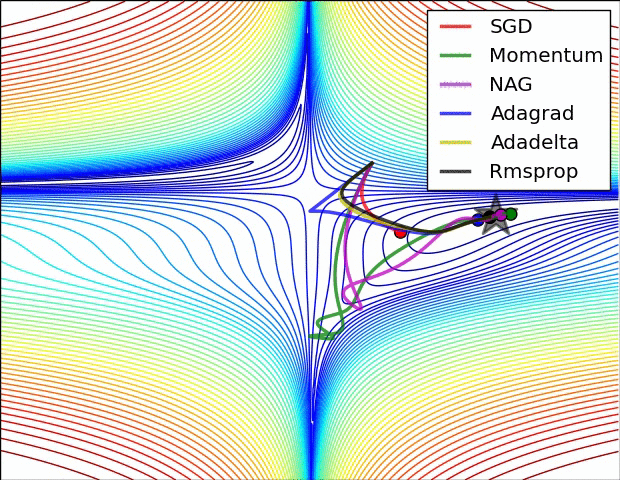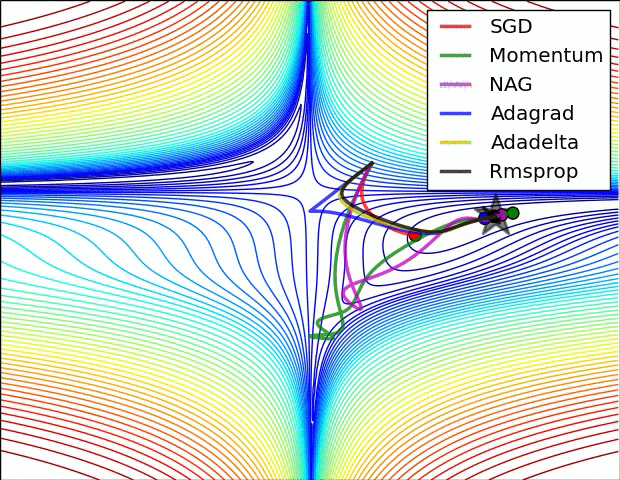
下图展示了各个算法在鞍点的情况。

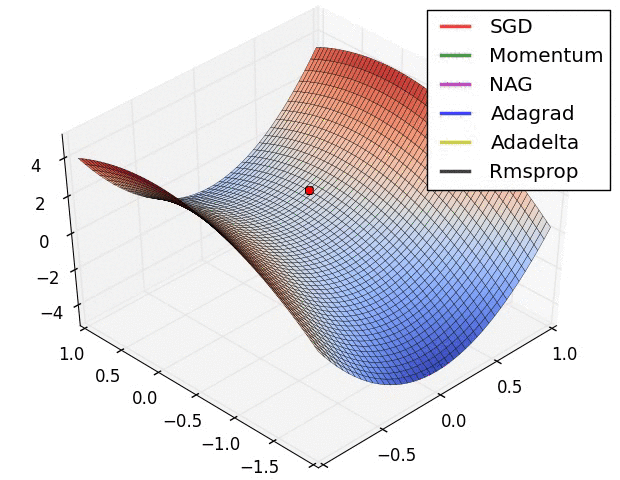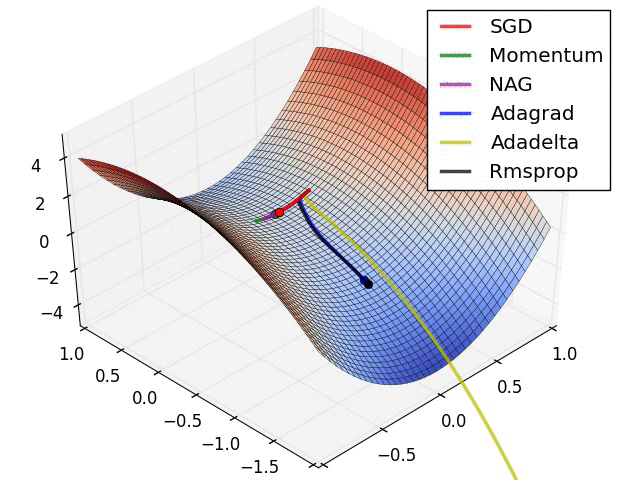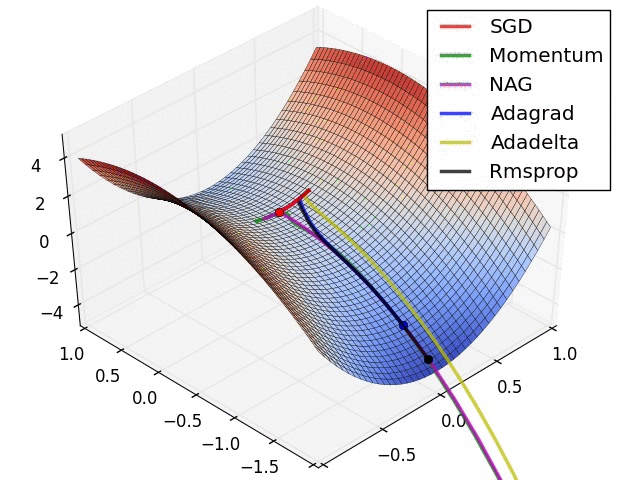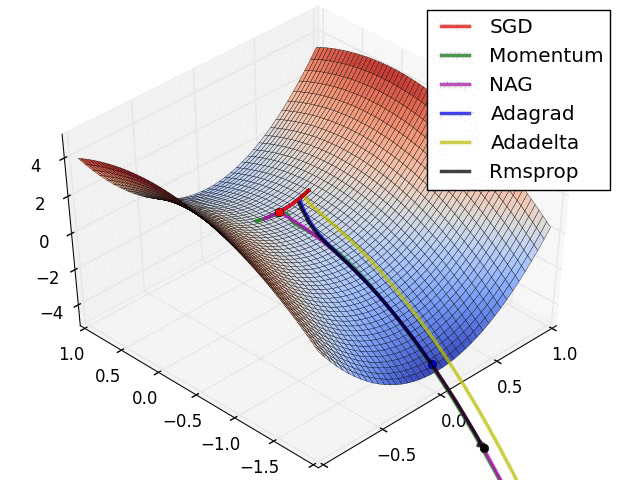
SGD, Momentum, NAG 很难逃离鞍点，而 Adagrad, Adadelta, Rmsprop 能够迅速逃离。

https://zhuanlan.zhihu.com/p/22252270
https://zhuanlan.zhihu.com/p/32230623
https://zhuanlan.zhihu.com/p/22810533
http://wowx.info/posts/401226963/
http://cs231n.github.io/optimization-1/
https://zhuanlan.zhihu.com/p/21486826 冲量，解释的很好
https://github.com/hsmyy/zhihuzhuanlan/blob/master/momentum.ipynb 画图
http://ruder.io/optimizing-gradient-descent/index.html
http://cs231n.github.io/neural-networks-3/
http://ruder.io/deep-learning-optimization-2017/
https://distill.pub/2017/momentum/